Задача «Геолокация по освещённости»

Задача

Обработать данные геолокатора фиксирующего освещенность, получить и визуализировать записанный трек.

Описание

Сезонные перелеты птиц традиционно изучаются при помощи кольцевания и наблюдений по маршруту миграции. Эти методы позволяют выяснить пути миграции лишь в самых общих чертах. C недавнего времени появилась возможность изготовлять совсем крошечные геолокаторы весом несколько грамм, которые не отягощают даже маленьких птичек.

Такой миниатюрный геолокатор умеет фиксировать изменения освещенности в реальном времени и вносит их в журнал. По этим данным можно определить время восхода и захода солнца и продолжительность дня, что в большинстве случаев позволяет вычислить географическое положение с приемлемой точностью.

трекинг полярных крачек

Смена времен года определяется движением Земли вокруг Солнца. Смена суток — вращением Земли вокруг своей оси. Для расчета времени захода и восхода солнца в любом месте планеты в любой день года необходимо иметь математическое описание обоих движений.

Годовое движение Земли

Земля движется вокруг Солнца по эллиптической орбите. Форма эллипса и положение Земли на нём определяются с помощью 6 параметров — Кеплеровых элементов орбиты.

В таблице ниже приведены значения элементов орбиты Земли:


большая полуось	(а.е.)	a =	1.00000261	+ 0.00000562 t
эксцентриситет		e =	0.01671123	‒ 0.00004392 t
наклон к эклиптике	(°)	i =	0.0
аргумент перигелия	(°)	ω =	102.93768193	+ 0.32327364 t
долгота восходящего узла	(°)	Ω =	0.0
средняя аномалия	(°)	M =	357.52688973	+ 35999.04917617 t

Здесь t — это время в столетиях, прошедшее с 12:00 UTC 1 января 2000 г. (столетие считаем = 36525 дней). Формула для вычисления t из времени Unix:

t = (t_unix ‒ 946728000) / 3155760000

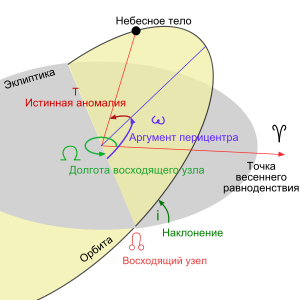
Расчет движения планеты по эллиптической орбите производится в гелиоцентрической системе координат, связанной с плоскостью орбиты (начало координат — центр Солнца, базовая плоскость — плоскость орбиты, ось x направлена к перигею орбиты). Здесь нужно добавить, что в случае Земли, плоскость орбиты совпадает с плоскостью эклиптики.

движение по эллиптической орбите

Для расчета используют равномерно изменяющийся во времени угол M называемый средней аномалией (∠SOD на рисунке обозначен зелёным). При M = 0° планета находится в ближайшей к солнцу точке орбиты — перигелии, при M = 180° — в апогее.

Истинная аномалия T — угол между планетой (точка B на рисунке), Солнцем (точка S на рисунке) и точкой перигелия — не совпадает с M, кроме моментов прохождения планетой перигелия и апогея.

Для расчета положения планеты на орбите вводят еще один угол — эксцентрическую аномалию E (∠SOC на рисунке обозначен красным):

$\tan \frac{E}{2} = \sqrt{ \frac{1-e}{1+e} } \tan \frac{ \text{T} }{2}$

Эксцентрическая аномалия E связана со средней аномалией M уравнением Кеплера:

$M = E - e \sin E$

Уравнение Кеплера является трансцендентным и не решается в алгебраических функциях. Для его численного решения применяют итеративный метод Ньютона:

$\begin{matrix} E_{0} = M + e \sin M \\ \left\{\begin{matrix} \Delta M = & M - (E_{n} - e \sin E_{n}) \\ \Delta E = & \Delta M / (1 - e \cos E_{n})\\ E_{n+1} = & E_{n} + \Delta E \end{matrix}\right. \end{matrix}$

Вычисления останавливаются по достижении приемлемой точности: $\left | \Delta E \right | < 0.000001^{\circ}$

Вычисленная эксцентрическая аномалия E позволяет рассчитать координаты планеты:

$\begin{matrix} x = & a (\cos E - e) & \\ y = & a \sqrt{1-e^2} \sin E \\ \end{matrix}$

После того как положение планеты вычислено, необходимо произвести несколько переходов из одной системы координат в другую.

В случае Земли плоскость орбиты совпадает с плоскостью эклиптики, а направление на восходящий узел орбиты совпадает с направлением на точку весеннего равноденствия, поэтому на первом этапе необходимо просто повернуть систему отсчета так, что бы ось x была направлена не на перигелий, а на точку весеннего равноденствия. Для этого перехода необходимо произвести поворот вокруг оси z на угол ω.

То есть исходный вектор

$\vec r = \overrightarrow{ (x, y, 0) }$

требуется умножить на матрицу поворота:

$\vec r_{\varepsilon} = Rot_{z}( \omega ) \vec r$

Затем перейдем из гелиоцентрической системы (начало координат — центр Солнца, базовая плоскость — эклиптика, ось x направлена к точке весеннего равноденствия) в геоцентрическую (начало координат — центр Земли, базовая плоскость — эклиптика, ось x направлена к точке весеннего равноденствия), и вычислим координаты центра Солнца относительно центра Земли.

$\vec r_{\bigodot \varepsilon} = -\vec r_{\varepsilon}$

И, наконец, перейдём в систему координат, связанную с плоскостью земного экватора (начало координат — центр Земли, базовая плоскость — экватор, ось x направлена к точке весеннего равноденствия). Угол наклона эклиптики к плоскости земного экватора:

ε = 23.43926469° ‒ 0.01294668° t

Произведем поворот вектора вокруг оси x на угол ε:

$\vec r_{\bigodot \text{eq}} = Rot_{x}( \varepsilon ) \vec r_{\bigodot \varepsilon}$

Итого:

$\vec r_{\bigodot \text{eq}} = -Rot_{x}( \varepsilon ) Rot_{z}( \omega ) \vec r$

Вращение Земли

Координат Солнца, вычисленных относительно центра Земли, недостаточно для описания видимого положения Солнца: в один и тот же момент времени наблюдатели в разных местах планеты могут видеть восход, заход Солнца, его расположение на различной высоте как над, так и под горизонтом.

Для вычисления видимого положения Солнца необходимо перейти в систему координат, связанную с наблюдателем, находящимся в некоторой точке на поверхности Земли (начало координат — точка на поверхности планеты, базовая плоскость — плоскость горизонта, ось x будет направлена на юг, ось z — вверх, в зенит). Эта система вращается вместе с планетой и в каждый момент времени повёрнута вместе с ней вокруг оси вращения на некоторый, требующий вычисления, угол.

Для численного описания вращения Земли используется понятие звёздного времени. По сути, звездное время — это угол, откладываемый из центра Земли между точкой весеннего равноденствия и точкой на экваторе Земли. Звёздное время для нулевого (Гринвичского) меридиана называется Гринвичским звёздным временем и вычисляется по формуле:

s₀ = 280.460618375° + 13185000.77005360° t + 0.00038793° t² ‒ 0.0000000258° t³

Звёздное время для любой другой долготы: s = s₀ + λ, здесь λ > 0 для восточной долготы и λ < 0 — для западной.

Для перехода в систему отсчета наблюдателя, находящегося на поверхности земли в точке с координатами (λ, φ) необходимо произвести 3 преобразования:

поворот на угол s вокруг оси z (оси вращения планеты),
поворот на угол 90° ‒ φ вокруг оси y (переход на широту места наблюдения),
смещение вдоль оси z на радиус Земли R_E.

$\vec r_{\bigodot \text{local}} = Rot_{y} (-(90^{\circ}-\varphi)) Rot_{z} (-(s_{0}+\lambda)) \vec r_{\bigodot \text{eq}} + \overrightarrow{(0,0,R_{E})}$

Эта формула позволит найти угловую высоту центра Солнца в заданный момент времени в некоторой точке на планете. Для нашей задачи, наоборот, необходимо найти места на планете, где Солнце в данный момент видно на определённой высоте.

Переведем экваториальные и локальные координаты Солнца в сферическую форму.

$\vec r_{\bigodot \text{eq}} = \begin{pmatrix} x_{\text{eq}} \\ y_{\text{eq}} \\ z_{\text{eq}} \end{pmatrix} \Rightarrow \begin{matrix} \tan \alpha = \frac{ y_{\text{eq}} }{ x_{\text{eq}} }\text{,} & \tan \delta = \frac{ z_{\text{eq}} }{ \sqrt{ x_{\text{eq}}^2 + y_{\text{eq}}^2 } }\text{,} & r = \sqrt{ x_{\text{eq}}^2 + y_{\text{eq}}^2 + z_{\text{eq}}^2 } \end{pmatrix}$

$\vec r_{\bigodot \text{local}} = \begin{pmatrix} x_{\text{local}} \\ y_{\text{local}} \\ z_{\text{local}} \end{pmatrix} \Rightarrow \begin{matrix} \tan A = \frac{ y_{\text{local}} }{ -x_{\text{local}} }\text{,} & \tan h = \frac{ z_{\text{local}} }{ \sqrt{ x_{\text{local}}^2 + y_{\text{local}}^2 } }\text{,} & r{'} = \sqrt{ x_{\text{local}}^2 + y_{\text{local}}^2 + z_{\text{local}}^2 } \end{pmatrix}$

Здесь α, δ, r — геоцентрические сферические координаты центра Солнца, A — азимут, h — угловая высота центра Солнца над горизонтом в точке наблюдения.

Развернув формулы, произведя несложные тригонометрические подстановки, и отбросив R_E за малостью по сравнению с расстоянием до Солнца, получим формулу для расчета высоты Солнца:

$\sin h = \cos \varphi \cos \delta \cos ( \alpha - (s_{0} + \lambda) ) + \sin \varphi \sin \delta$

Моментом восхода Солнца считается момент пересечения верхнего края диска линии горизонта, что, с учётом углового размера Солнца, а также рефракции атмосферы, даёт h₀ = ‒0.835° — угловая высота центра Солнца в момент восхода/захода. Отсюда следует:

$\cos ( ( \alpha - s_{0} ) - \lambda ) = \frac{ -0.0145439 - \sin \varphi \sin \delta }{ \cos \varphi \cos \delta }$

или $\lambda = \alpha - s_{0} \pm \Delta \lambda$ , где

$\Delta \lambda = \arccos \left ( \frac{ -0.0145439 - \sin \varphi \sin \delta }{ \cos \varphi \cos \delta} \right )$

Сравнивая два смежные записи о восходе и заходе Солнца можно оценить геометрическое место точек на планете, где эти записи могли быть сделаны.

Долгота дня в часах оценивается из соотношения: $d = \frac{ 2 \Delta \lambda }{ 15^{\circ} }$

Этих сведений достаточно, чтобы найти и оценить местоположение объекта на поверхности Земли по временам восхода и захода Солнца.

По материалам: jpl.nasa.gov, usno.navy.mil

Замечания по реализации

Вычисления движения и вращения Земли реализуются в классе SolarVisibility со следующим функционалом:

расчет координат Солнца на заданную дату,
расчет широты φ восхода/захода солнца для заданной долготы λ
расчет долготы λ восхода/захода солнца для заданной широты φ

Поиск координат трекера реализуются в классе TrackSolver. Методы класса пробегают вектор входных данных и строят результирующий вектор с датами, гео-точками, и оценками ошибок.

Исходные данные

Знак - означает заход, + — восход Солнца. Все времена — UTC.

- 2010-08-14 22:54
+ 2010-08-15 06:43
- 2010-08-15 22:54
+ 2010-08-16 06:49
- 2010-08-16 22:49
+ 2010-08-17 06:51
- 2010-08-17 22:42
+ 2010-08-18 06:53
- 2010-08-18 22:35
+ 2010-08-19 06:56
- 2010-08-19 22:31
+ 2010-08-20 07:17
- 2010-08-20 22:14
+ 2010-08-21 07:23
- 2010-08-21 22:12
+ 2010-08-22 07:50
- 2010-08-22 22:03
+ 2010-08-23 08:12
- 2010-08-23 22:15
+ 2010-08-24 08:13
- 2010-08-24 22:10
+ 2010-08-25 08:19
- 2010-08-25 22:12
+ 2010-08-26 08:19
- 2010-08-26 22:07
+ 2010-08-27 08:17
- 2010-08-27 22:03
+ 2010-08-28 08:22
- 2010-08-28 22:05
+ 2010-08-29 08:26
- 2010-08-29 22:04
+ 2010-08-30 08:25
- 2010-08-30 21:57
+ 2010-08-31 08:25
- 2010-08-31 21:50
+ 2010-09-01 08:22
- 2010-09-01 21:48
+ 2010-09-02 08:25
- 2010-09-02 21:43
+ 2010-09-03 08:28
- 2010-09-03 21:42
+ 2010-09-04 08:28
- 2010-09-04 21:39
+ 2010-09-05 08:28
- 2010-09-05 21:35
+ 2010-09-06 08:33
- 2010-09-06 21:33
+ 2010-09-07 08:31
- 2010-09-07 21:28
+ 2010-09-08 08:31
- 2010-09-08 21:28
+ 2010-09-09 08:36
- 2010-09-09 21:31
+ 2010-09-10 08:41
- 2010-09-10 21:25
+ 2010-09-11 08:36
- 2010-09-11 21:23
+ 2010-09-12 08:38
- 2010-09-12 21:21
+ 2010-09-13 08:38
- 2010-09-13 21:16
+ 2010-09-14 08:39
- 2010-09-14 21:13
+ 2010-09-15 08:43
- 2010-09-15 21:09
+ 2010-09-16 08:38
- 2010-09-16 21:04
+ 2010-09-17 08:40
- 2010-09-17 21:05
+ 2010-09-18 08:43
- 2010-09-18 21:00
+ 2010-09-19 08:43
- 2010-09-19 20:50
+ 2010-09-20 08:32
- 2010-09-20 20:32
+ 2010-09-21 08:14
- 2010-09-21 20:05
+ 2010-09-22 07:47
- 2010-09-22 19:52
+ 2010-09-23 07:38
- 2010-09-23 19:31
+ 2010-09-24 07:14
- 2010-09-24 19:15
+ 2010-09-25 07:08
- 2010-09-25 19:07
+ 2010-09-26 07:16
- 2010-09-26 19:15
+ 2010-09-27 07:13
- 2010-09-27 19:25
+ 2010-09-28 07:26
- 2010-09-28 19:22
+ 2010-09-29 07:14
- 2010-09-29 19:12
+ 2010-09-30 07:01
- 2010-09-30 19:09
+ 2010-10-01 06:55
- 2010-10-01 18:46
+ 2010-10-02 06:30
- 2010-10-02 18:23
+ 2010-10-03 06:04
- 2010-10-03 18:00
+ 2010-10-04 05:42
- 2010-10-04 17:38
+ 2010-10-05 05:18
- 2010-10-05 17:18
+ 2010-10-06 05:01
- 2010-10-06 17:22
+ 2010-10-07 04:59
- 2010-10-07 17:24
+ 2010-10-08 04:56
- 2010-10-08 17:18
+ 2010-10-09 04:43
- 2010-10-09 17:22
+ 2010-10-10 04:29
- 2010-10-10 17:09
+ 2010-10-11 04:33
- 2010-10-11 17:38
+ 2010-10-12 04:57
- 2010-10-12 18:02
+ 2010-10-13 05:23
- 2010-10-13 18:21
+ 2010-10-14 05:43
- 2010-10-14 18:39
+ 2010-10-15 05:50
- 2010-10-15 19:02
+ 2010-10-16 05:48
- 2010-10-16 19:08
+ 2010-10-17 06:01
- 2010-10-17 19:24
+ 2010-10-18 06:06
- 2010-10-18 19:38
+ 2010-10-19 06:14
- 2010-10-19 19:45
+ 2010-10-20 06:16
- 2010-10-20 20:05
+ 2010-10-21 06:11
- 2010-10-21 19:53
+ 2010-10-22 06:00
- 2010-10-22 19:44
+ 2010-10-23 05:40
- 2010-10-23 19:55
+ 2010-10-24 05:05
- 2010-10-24 20:13
+ 2010-10-25 05:05
- 2010-10-25 20:45
+ 2010-10-26 04:30
- 2010-10-26 20:45
+ 2010-10-27 03:43
- 2010-10-27 21:32
+ 2010-10-28 03:34
- 2010-10-28 21:58
+ 2010-10-29 04:02
- 2010-10-29 22:34
+ 2010-10-30 04:15
- 2010-10-30 22:14
+ 2010-10-31 03:51
- 2010-10-31 22:24
+ 2010-11-01 04:30
- 2010-11-01 23:15
+ 2010-11-02 04:20
- 2010-11-02 23:10
+ 2010-11-03 04:28
- 2010-11-03 23:20
+ 2010-11-04 04:39
- 2010-11-04 23:15
+ 2010-11-05 04:11
- 2010-11-05 23:18
+ 2010-11-06 03:50
- 2010-11-06 23:18
+ 2010-11-07 04:28
- 2010-11-07 23:37
+ 2010-11-08 04:36
- 2010-11-09 00:01
+ 2010-11-09 04:37
- 2010-11-10 00:10
+ 2010-11-10 04:17
- 2010-11-11 00:13
+ 2010-11-11 04:15
- 2010-11-12 00:15
+ 2010-11-12 04:16
- 2010-11-13 00:23
+ 2010-11-13 03:57
- 2010-11-14 00:19
+ 2010-11-14 03:54
- 2010-11-15 00:20
+ 2010-11-15 04:00
- 2010-11-16 00:36
+ 2010-11-16 03:44
- 2010-11-17 01:04
+ 2010-11-17 03:19
- 2010-11-18 00:59
+ 2010-11-18 03:23
- 2010-11-19 00:51
+ 2010-11-19 03:23
- 2010-11-20 00:53
+ 2010-11-20 03:13
- 2010-11-21 01:08
+ 2010-11-21 02:58
- 2010-11-22 01:18
+ 2010-11-22 02:46

Блок задач

Темы

Сложность 6