Задача «Изменение размера изображения»

Реализовать изменение размеров (ресэмплинг) изображения.

Входные данные

ВMP файл

Справочная информация

Изображение - это непрерывная функция цвета от координат, c(x,y). При переводе изображения в цифровую форму происходит дискретизация и квантование изначально непрерывной функции c(x,y). Непрерывное изображение разделяется на одинаковые прямоугольные области. Каждой такой области сопоставляется значение цвета, взятое в её средней точке. В результате получается набор отсчетов, собранный в двумерный массив d(i,j).

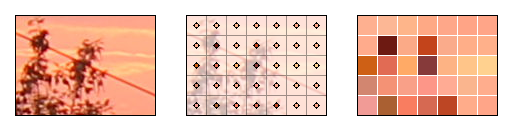
дискретизация 7x5

Часто возникает необходимость получить то же самое цифровое изображение в другом разрешении: большем или меньшем. Если в наличии есть исходное непрерывное изображение c(x,y), то достаточно повторно провести дискретизацию с другим шагом по горизонтали и вертикали.

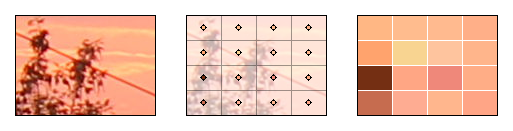
дискретизация 4x4

дискретизация 10x10

Но чаще всего в наличии есть только цифровое изображение: массив отсчетов d(i,j). В этом случае, необходимо на основании этих отсчетов воссоздать (интерполировать) непрерывное изображение c'(x,y), а затем провести его повторную дискретизацию с требуемыми параметрами.

Естественно, построенное с помощью интерполяции изображение c'(x,y), может, и часто будет не совпадать в деталях с исходным c(x,y) (теорема Котельникова).

Для задачи передискретизации достаточно вычислить значения функции c'(x,y) только в нужных точках, и из полученных отсчетов сформировать новое цифровое изображение r(i,j).

передискретизация 4x4

передискретизация 10x10

Интерполированное значение цвета в произвольной точке c'(x,y) можно представить как линейную комбинацию отсчетов d(i,j) в некоторой окрестности искомой точки.

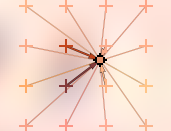
интерполяция значения ${c}'(x,y) = \sum_{i,j} d(i,j)W(i-x)W(j-y)$

Формула "веса" W(x) выбирается в зависимости от используемого алгоритма интерполяции. Также в зависимости от выбранного алгоритма может быть различно число используемых "окрестных" отсчетов.

Билинейная интерполяция

$W(x) = \begin{cases} 1-\left | x \right | & \left | x \right |<1 \\ 0 & \text{otherwise} \end{cases}$

линейная интерполяция

При интерполяции изображения используются 4 ближайших известных точки (по 1 отсчету в каждом направлении по каждой оси).

Бикубическая интерполяция

$W(x) = \begin{cases} +\frac{1}{2}\left (\left | x \right |^2-1 \right)\left (\left | x \right |-2 \right ) & \left | x \right |<1 \\ -\frac{1}{6}\left (\left | x \right | -1 \right)\left (\left | x \right |-2 \right )\left (\left | x \right |-3 \right ) & 1< \left | x \right |<2 \\ 0 & \text{otherwise} \end{cases}$

кубическая интерполяция

При интерполяции изображения используются 16 ближайших известных точек (по 2 отсчета в каждом направлении по каждой оси).

Интерполяция Ланцоша

$W_{a}(x) = \begin{cases} 1 & t = 0 \\ \mathrm{sinc}(x)\, \mathrm{sinc} \! \left( \frac x a \right) & \left | t \right | < a \\ 0 & \text{otherwise} \end{cases}$

Для интерполяции изображений обычно используют a = 2 или a = 3.

интерполяция Ланцоша 2 интерполяция Ланцоша 3

При a = 2 используются 16 ближайших известных точек (по 2 отсчета в каждом направлении по каждой оси), при a = 3 - 36 ближайших точек (по 3 отсчета в каждом направлении по каждой оси).

Постановка задачи

Реализовать изменение размеров (ресэмплинг) изображения на базе алгоритмов билинейной, бикубической интерполяции и фильтрации Ланцоша.

Выходные данные

BMP файл

Блок задач

Темы

Сложность 6